AI Assistants to Grow Your Business
Our Offering
AI Salesman
AI Community Manager
AI Copywriter
AI Analyst
Engage More, Market More
Time on site
Conversion rate
More sales

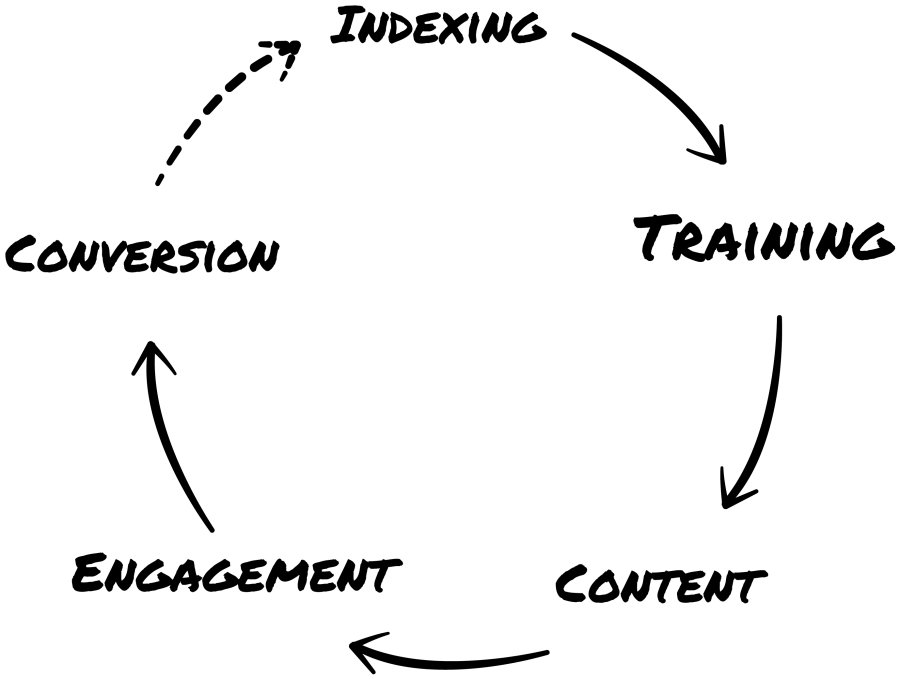
How Does HAL149 Work?
- Indexing. Translation of contents into vector indexes.
- Prompting, fine-tuning and embedding techniques.
- Create and publish online posts.
- Engagement. Engaging with users in natural language.
- Conversion. Extracting data and leads from interactions.
FAQs
HAL149 stands out due to the training of its assistants and the specialisation of its tools.
Each AI model is trained 24×7 at both the business sector and customer level, resulting in accurate interactions and preventing hallucinations.
Furthermore, HAL149’s offering is organised around specialised tools, ensuring complete customisation for each client.
Typically, training involves using a corpus of data consisting of online content and business documents.
This information is adapted by an AI Trainer and integrated into the client’s model using various procedures.
Training on industry information is ongoing. We will be updating information on this training for specific industries and topics in the coming weeks.
The training time depends on the format (PDFs, Word, etc.) and the amount of information in your company.
Ongoing training with sector information is conducted by crawling news items, which are then incorporated into the IA Assistant.
ChatGPT only has access to the information used in the fine-tuning training process of the AI Assistant.
For company data we use a separate index using the embeddings training procedure.
This ensures the separation of the base model while maintaining the reliability of the answers.

On our Blog
AI Wars and the Role of Entrepreneurs
Entrepreneurs face a unique challenge. As large companies push into the AI field, it may seem that the natural competitive advantage of startups – agility […]
Building AI products in the ChatGPT era: Am I too late?
You may think you missed the boat on the AI behind ChatGPT, but the truth is, the field is still nascent. OpenAI only had around […]
Artificial Intelligence to Generate Business Ideas?
Artificial intelligence (AI) is revolutionising the way we interact with technology, offering creative solutions and even making it possible to generate business ideas in ways […]
